simhash与重复信息识别
随着信息爆炸时代的来临,互联网上充斥着着大量的近重复信息,有效地识别它们是一个很有意义的课题。例如,对于搜索引擎的爬虫系统来说,收录重复的网页是毫无意义的,只会造成存储和计算资源的浪费;同时,展示重复的信息对于用户来说也并不是最好的体验。
造成网页近重复的可能原因主要包括:
- 镜像网站
- 内容复制
- 嵌入广告
- 计数改变
- 少量修改
一个简化的爬虫系统架构如下图所示:
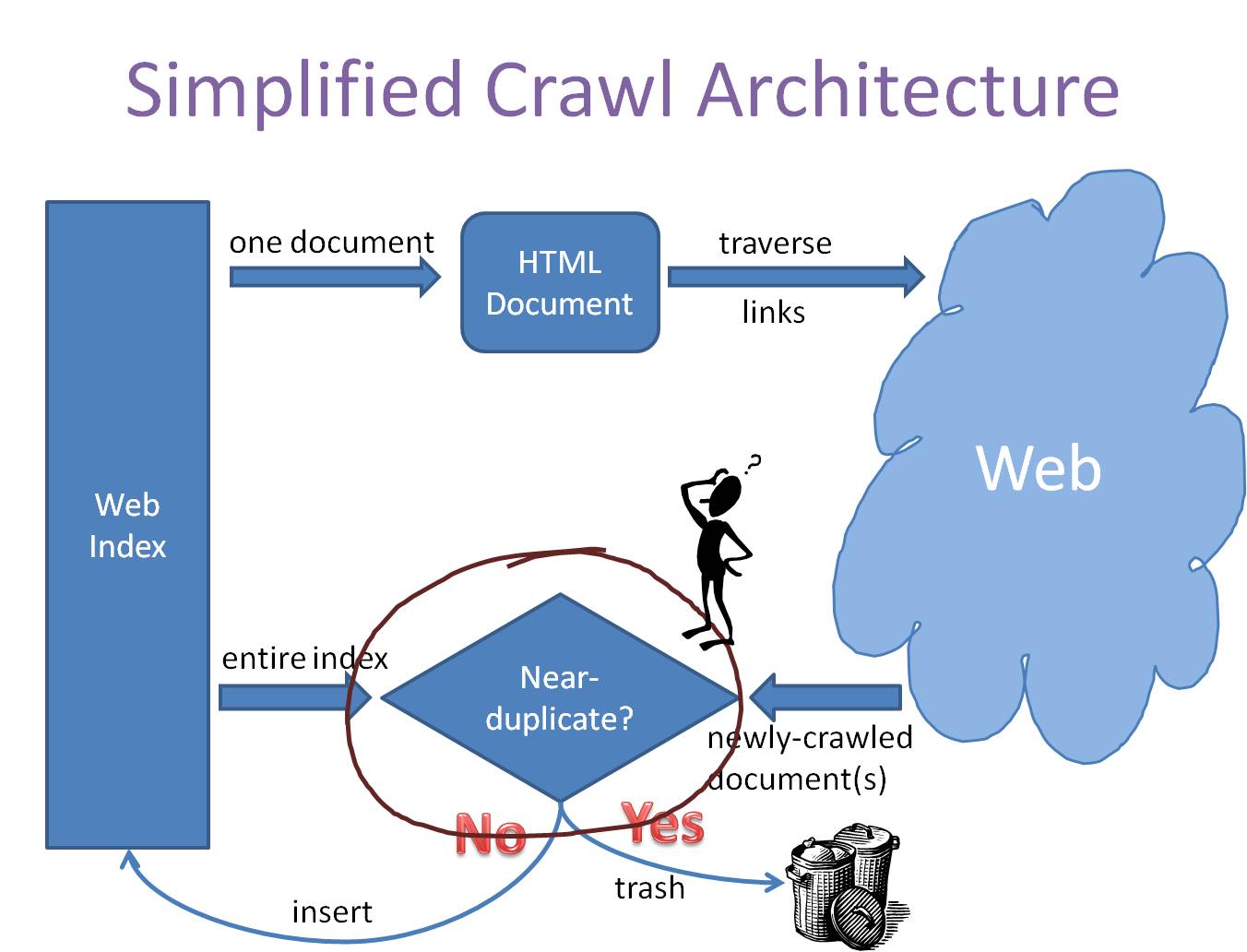
事实上,传统比较两个文本相似性的方法,大多是将文本分词之后,转化为特征向量距离的度量,比如常见的欧氏距离、海明距离或者余弦角度等等。两两比较固然能很好地适应,但这种方法的一个最大的缺点就是,无法将其扩展到海量数据。例如,试想像Google那种收录了数以几十亿互联网信息的大型搜索引擎,每天都会通过爬虫的方式为自己的索引库新增的数百万网页,如果待收录每一条数据都去和网页库里面的每条记录算一下余弦角度,其计算量是相当恐怖的。
我们考虑采用为每一个web文档通过hash的方式生成一个指纹(fingerprint)。传统的加密式hash,比如md5,其设计的目的是为了让整个分布尽可能地均匀,输入内容哪怕只有轻微变化,hash就会发生很大地变化。我们理想当中的哈希函数,需要对几乎相同的输入内容,产生相同或者相近的hashcode,换句话说,hashcode的相似程度要能直接反映输入内容的相似程度。很明显,前面所说的md5等传统hash无法满足我们的需求。
simhash是locality sensitive hash(局部敏感哈希)的一种,最早由Moses Charikar在《similarity estimation techniques from rounding algorithms》一文中提出。Google就是基于此算法实现网页文件查重的。我们假设有以下三段文本: the cat sat on the mat the cat sat on a mat we all scream for ice cream
使用传统hash可能会产生如下的结果:
irb(main):006:0> p1 = 'the cat sat on the mat'
irb(main):005:0> p2 = 'the cat sat on a mat'
irb(main):007:0> p3 = 'we all scream for ice cream'
irb(main):007:0> p1.hash => 415542861
irb(main):007:0> p2.hash => 668720516
irb(main):007:0> p3.hash => 767429688
使用simhash会应该产生类似如下的结果:
irb(main):003:0> p1.simhash => 851459198 00110010110000000011110001111110
irb(main):004:0> p2.simhash => 847263864 00110010100000000011100001111000
irb(main):002:0> p3.simhash => 984968088 00111010101101010110101110011000
海明距离的定义,为两个二进制串中不同位的数量。上述三个文本的simhash结果,其两两之间的海明距离为(p1,p2)=4,(p1,p3)=16以及(p2,p3)=12。事实上,这正好符合文本之间的相似度,p1和p2间的相似度要远大于与p3的。
如何实现这种hash算法呢?以上述三个文本为例,整个过程可以分为以下六步:
1、选择simhash的位数,请综合考虑存储成本以及数据集的大小,比如说32位
2、将simhash的各位初始化为0
3、提取原始文本中的特征,一般采用各种分词的方式。比如对于"the cat sat on the mat",采用两两分词的方式得到如下结果:{"th", "he", "e ", " c", "ca", "at", "t ", " s", "sa", " o", "on", "n ", " t", " m", "ma"}
4、使用传统的32位hash函数计算各个word的hashcode,比如:"th".hash = -502157718 ,"he".hash = -369049682,……
5、对各word的hashcode的每一位,如果该位为1,则simhash相应位的值加1;否则减1
6、对最后得到的32位的simhash,如果该位大于1,则设为1;否则设为0
整个过程可以参考下图:

按照Charikar在论文中阐述的,64位simhash,海明距离在3以内的文本都可以认为是近重复文本。当然,具体数值需要结合具体业务以及经验值来确定。
使用上述方法产生的simhash可以用来比较两个文本之间的相似度。问题是,如何将其扩展到海量数据的近重复检测中去呢?譬如说对于64位的待查询文本的simhash code来说,如何在海量的样本库(>1M)中查询与其海明距离在3以内的记录呢?下面在引入simhash的索引结构之前,先提供两种常规的思路。
第一种是方案是查找待查询文本的64位simhash code的所有3位以内变化的组合,大约需要四万多次的查询,参考下图:
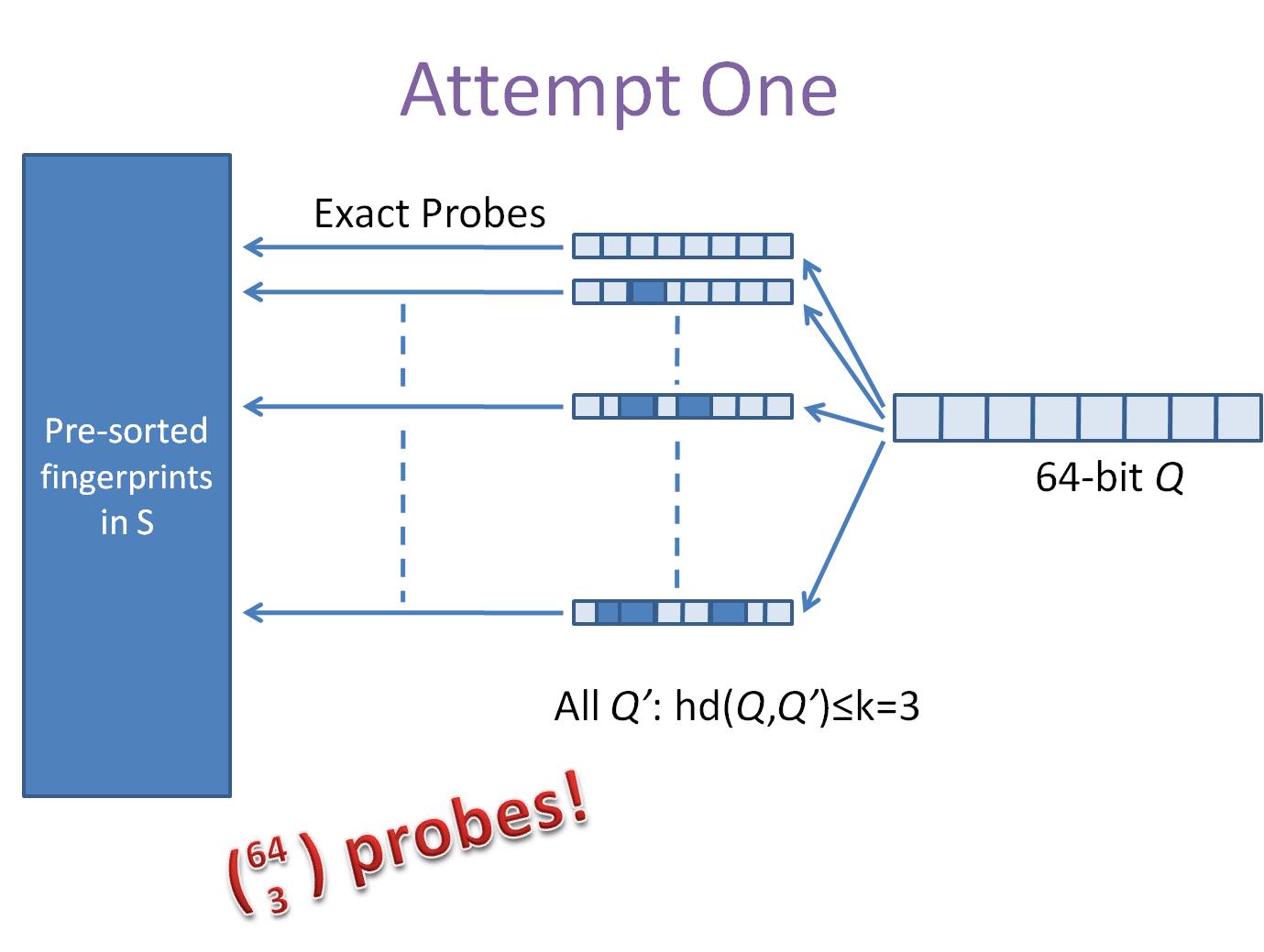
另一种方案是预生成库中所有样本simhash code的3位变化以内的组合,大约需要占据4万多倍的原始空间,参考下图:
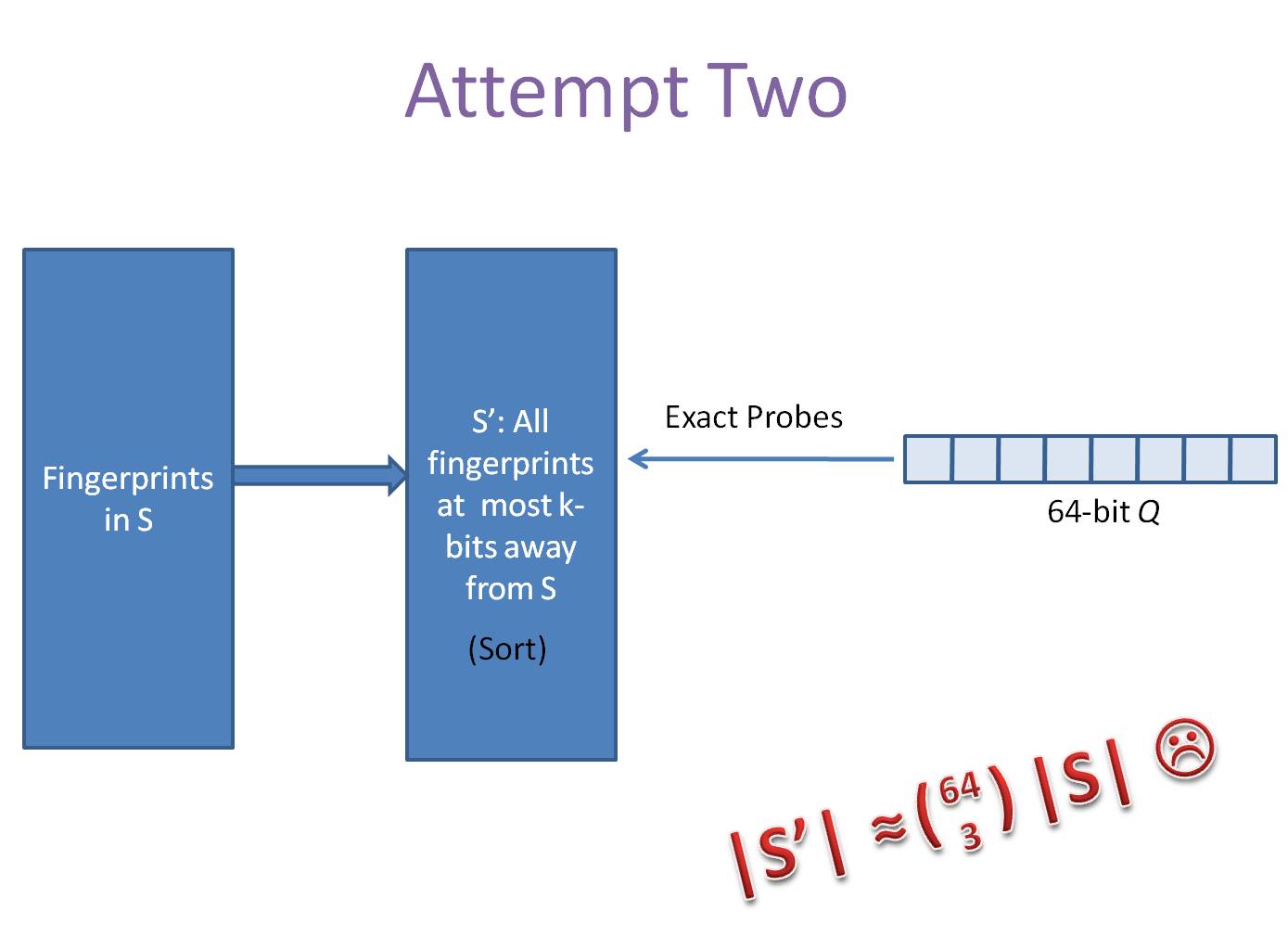
显然,上述两种方法,或者时间复杂度,或者空间复杂度,其一无法满足实际的需求。我们需要一种方法,其时间复杂度优于前者,空间复杂度优于后者。
假设我们要寻找海明距离3以内的数值,根据抽屉原理,只要我们将整个64位的二进制串划分为4块,无论如何,匹配的两个simhash code之间至少有一块区域是完全相同的,如下图所示:
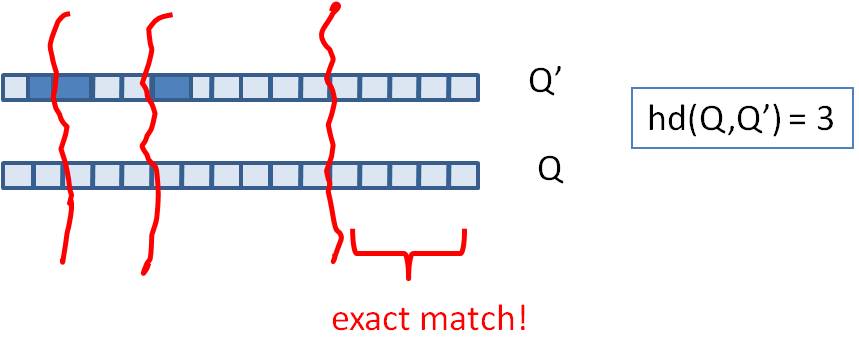
由于我们无法事先得知完全相同的是哪一块区域,因此我们必须采用存储多份table的方式。
在本例的情况下,我们需要存储4份table,并将64位的simhash code等分成4份;对于每一个输入的code,我们通过精确匹配的方式,查找前16位相同的记录作为候选记录,如下图所示:

让我们来总结一下上述算法的实质:
1、将64位的二进制串等分成四块
2、调整上述64位二进制,将任意一块作为前16位,总共有四种组合,生成四份table
3、采用精确匹配的方式查找前16位
4、如果样本库中存有2^34(差不多10亿)的哈希指纹,则每个table返回2^(34-16)=262144个候选结果,大大减少了海明距离的计算成本
我们可以将这种方法拓展成多种配置,不过,请记住,table的数量与每个table返回的结果呈此消彼长的关系,也就是说,时间效率与空间效率不可兼得,参看下图:

事实上,这就是Google每天所做的,用来识别获取的网页是否与它庞大的、数以十亿计的网页库是否重复。另外,simhash还可以用于信息聚类、文件压缩等。
也许,读到这里,你已经感受到数学的魅力了。
simhash与Google的网页去重
Simhash
传统IR领域内文本相似度比较所采用的经典方法是文本相似度的向量夹角余弦,其主要思想是根据一个文章中出现词的词频构成一个向量,然后计算两篇文章对应向量的向量夹角。但由于有可能一个文章的特征向量词特别多导致整个向量维度很高,使得计算的代价太大,对于Google这种处理万亿级别的网页的搜索引擎而言是不可接受的,
simhash算法的主要思想是降维,将高维的特征向量映射成一个f-bit的指纹(fingerprint),通过比较两篇文章的f-bit指纹的Hamming Distance来确定文章是否重复或者高度近似。 simhash算法很精巧,但却十分容易理解和实现,具体的simhash过程如下:
- 首先基于传统的IR方法,将文章转换为一组加权的特征值构成的向量。
2.初始化一个f维的向量V,其中每一个元素初始值为0。
3.对于文章的特征向量集中的每一个特征,做如下计算: 利用传统的hash算法映射到一个f-bit的签名。对于这个f- bit的签名,如果签名的第i位上为1,则对向量V中第i维加上这个特征的权值,否则对向量的第i维减去该特征的权值。
4.对整个特征向量集合迭代上述运算后,根据V中每一维向量的符号来确定生成的f-bit指纹的值,如果V的第i维为正数,则生成f-bit指纹的第i维为1,否则为0。
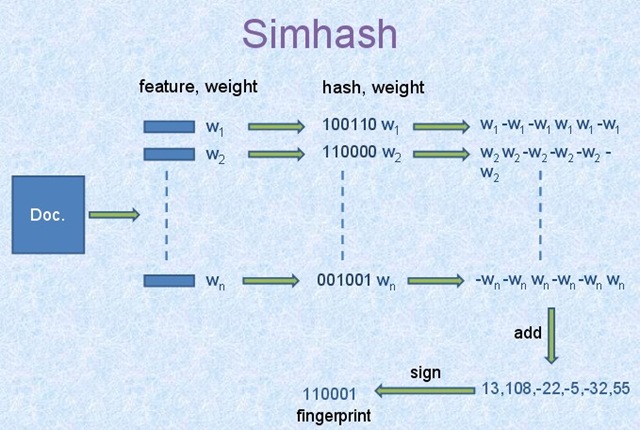
simhash和普通hash最大的不同在于传统的hash函数虽然也可以用于映射来比较文本的重复,但是对于可能差距只有一个字节的文档也会映射成两个完全不同的哈希结果,而simhash对相似的文本的哈希映射结果也相似。Google的论文中取了f=64,即将整个网页的加权特征集合映射到一个64-bit的fingerprint上。
比起simhash,整片文章中Google所采用的查找与给定f-bit的fingerprint的海明距离(Hamming Distance)小于k的算法相对还稍微难理解点。
fingerprint的Hamming Distance
问题:一个80亿的64-bit指纹组成的集合Q,对于一个给定64-bit的指纹F,如何在a few millionseconds中找到Q中和f至多只有k(k=3)位差别的指纹。
思想:
- 对于一个具有2^d个记录的集合,只需要考虑d-bit hash。
- 选取一个d’使得|d’-d|十分小,因此如果两fingerprint在d’-bits上都相同,那么在d-bits也很可能相同。然后在这些d-bit match的结果中寻找整个f-bit的Hamming Distance小于k的fingerprint。 简单的说,就是利用fingerprint少量特征位数比较从而首先缩小范围,然后再去确定是否差异小于k个bit。
算法的重点在于对于集合Q的分表以及每个表所对应的置换函数,假设对于64-bit的fingerprint,k=3,存储16个table,划分参考下图:
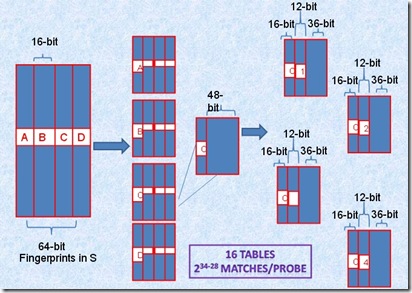
将64-bit按照16位划分为4个区间,每个区间剩余的48-bit再按照每个12-bit划分为4个区间,因此总共16个table并行查找,即使三个不同的k-bit落在A、B、C、D中三个不同的区块,此划分方法也不会导致遗漏。
以上方法是对于online的query,即一个给定的F在集合中查找相似的fingerprint。如果爬虫每天爬取了100w个网页,快速的查找这些新抓取的网页是否在原集合中有Near-duplication,对于这种batch-query的情况,Map-Reduce就发挥它的威力了。
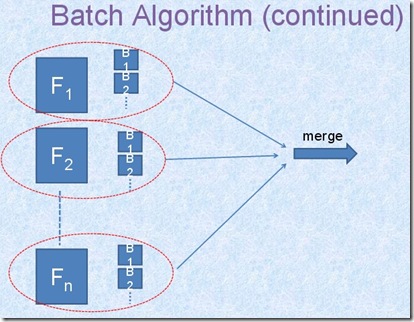
不同的是,在batch-query的处理中,是对待查集合B(1M个fingerprint)进行复制置换构建Table而非8B的目标集合,而在每一个chunkserver上对Fi(F为整个8B的fingerprint)在整个Table(B)中进行探测,每一个chunkserver上的的该Map过程输出该Fi中与整个B的near-duplicates,Reduces过程则将所有的结果收集、去重、然后输出为一个sorted file。
Haffman编码压缩
上述的查询过程,特别是针对online-version的算法,可以看出需要对8B的fingerprint进行多表复制和构建,其占据的容量是非常大的,不过由于构建的每一个置换Table都是sorted的,因此可以利用每一个fingerprint与其前一个的开始不同的bit-position h(h∈[0,f-1]) 来进行数据压缩,即如果前一个编码是11011011,而自身是11011001,则后一个可以编码为(6)1,即h=6,其中6表示从第6位(从0开始编号)开始和上一个fingerprint不相同(上一个为1,这个必然为0),然后再保存不相同位置右侧的编码,依次生成整个table。
Google首先计算整个排序的fingerprint表中h的分布情况,即不同的h出现次数,依据此对[0,f-1]上出现的h建立Haffman code,再根据上述规则生成table(例如上面的6就表示成对应的Haffman code)。其中table分为多个block,每一个block中的第一个fingerprint保存原数据,后面的依次按照编码生成。 将每一个block中所对应的最后一个fingerprint保存在内存中,因此在比对的时候就可以直接根据内存中的fingerprint来确定是哪一个block需要被decompress进行比较。 8B个64-bit的fingerprint原占据空间大约为64GB,利用上述Haffman code压缩后几乎会减少一般,而内存中又只对每一个block保存了一个fingerprint。